Metric dimension (graph theory)
In graph theory, the metric dimension of a graph G is the minimum number of vertices in a subset S of G such that all other vertices are uniquely determined by their distances to the vertices in S. Finding the metric dimension of a graph is an NP-hard problem; the decision version, determining whether the metric dimension is less than a given value, is NP-complete.
Contents |
Detailed definition
For an ordered subset 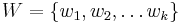 of vertices and a vertex v in a connected graph G, the representation of v with respect to W is the ordered k-tuple
of vertices and a vertex v in a connected graph G, the representation of v with respect to W is the ordered k-tuple 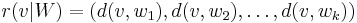 , where d(x,y) represents the distance between the vertices x and y. The set W is a resolving set (or locating set) for G if every two vertices of G have distinct representations. The metric dimension of G is the minimum cardinality of a resolving set for G. A resolving set containing a minimum number of vertices is called a basis (or reference set) for G. Resolving sets were introduced independently by Slater (1975) and Harary & Melter (1976).
, where d(x,y) represents the distance between the vertices x and y. The set W is a resolving set (or locating set) for G if every two vertices of G have distinct representations. The metric dimension of G is the minimum cardinality of a resolving set for G. A resolving set containing a minimum number of vertices is called a basis (or reference set) for G. Resolving sets were introduced independently by Slater (1975) and Harary & Melter (1976).
Trees
Slater (1975) provides the following simple characterization of the metric dimension of a tree. If the tree is a path, its metric dimension is one. Otherwise, let L denote the set of degree-one vertices in the tree (usually called leaves, although Slater uses that word differently). Let K be the set of vertices that have degree greater than two, and that are connected by paths of degree-two vertices to one or more leaves. Then the metric dimension is |L| − |K|. A basis of this cardinality may be formed by removing from L one of the leaves associated with each vertex in K.
Properties
In Chartrand, Eroh & Oellermann (2000), it is proved that:
- The metric dimension of a graph G is 1 if and only if G is a path.
- The metric dimension of an n-vertex graph is n − 1 if and only if it is a complete graph.
- The metric dimension of an n-vertex graph is n − 2 if and only if the graph is a complete bipartite graph Ks, t, a split graph
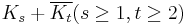 , or
, or 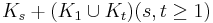 .
.
Khuller, Raghavachari & Rosenfeld (1996) prove the inequality 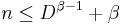 for any n-vertex graph with diameter D and metric dimension β.
for any n-vertex graph with diameter D and metric dimension β.
References
- Buczkowski, P.; Chartrand, G.; Poisson, C.; Zhang, P. (2003), "On k-dimensional graphs and their bases", Periodica Mathematica Hungarica 46 (1): 9–15, doi:10.1023/A:1025745406160, MR1975342.
- Chartrand, G.; Eroh, L.; Johnson, M. A.; Oellermann, O. R. (2000), "Resolvability in graphs and the metric dimension of a graph", Discrete & Applied Mathematics 105 (1–3): 99–113, doi:10.1016/S0166-218X(00)00198-0, MR1780464.
- Harary, F.; Melter, R. A. (1976), "On the metric dimension of a graph", Ars Combinatoria 2: 191–195, MR0457289.
- Slater, P. J. (1975), "Leaves of trees", Proc. 6th Southeastern Conference on Combinatorics, Graph Theory, and Computing (Florida Atlantic Univ., Boca Raton, Fla., 1975), Congressus Numerantium, 14, Winnipeg: Utilitas Math., pp. 549–559, MR0422062.
- Slater, P. J. (1988), "Dominating and reference sets in a graph", Journal of Mathematical and Physical Sciences 22 (4): 445–455, MR0966610.
- Khuller, S.; Raghavachari, B.; Rosenfeld, A. (1996), "Landmarks in graphs", Discrete Applied Math. 70 (3): 217–229, doi:10.1016/0166-218X(95)00106.
- Garey, M. R.; Johnson, D. S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5 A1.5: GT61, p. 204.